開集合と閉集合から見る「連結空間」とは

位相空間 \( X \) が連結であるとは、\( X \) の部分集合のうちで開集合かつ閉集合（クローペン集合）であるものが、全体集合 \( X \) と空集合 \( \emptyset \) だけであることを意味します。

つまり、空間の中に「一部だけ取り出しても開でも閉でもある」ような非自明な部分集合が存在しない場合、その空間は連結であるということです。

この考え方は、空間が一つにつながっているか、あるいは分断されているかを見極めるための基本的な基準になります。

なぜ重要なのか

位相空間で開集合と閉集合の両方の性質をもつ部分集合は、空間を二つの独立した領域に分離してしまう性質があります。

もし \( X \) でも \( \emptyset \) でもないクローペン集合が存在するなら、その空間は二つの交わらない非空の開集合に分けられ、連続的なつながりが失われます。つまり空間は非連結になります。

逆に、クローペン集合が \( X \) と \( \emptyset \) のみであれば、空間をそのように分割することはできません。この場合、空間は連結だと言えます。

補足：どんな位相空間でも、全体集合 \( X \) と空集合 \( \emptyset \) は常に開集合であり、同時に閉集合でもあります。

集合 \( X = \{ a, b, c, d \} \) に、次のような開集合族 \( T \) によって定まる位相を考えます。

\( T = \{ \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \} \)

離散位相空間におけるクローペン集合の例

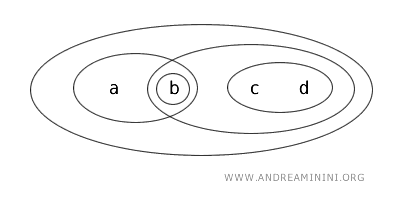
このとき、部分集合 \( \{ a, b \} \) はクローペン集合です。開集合の条件にも閉集合の条件にも当てはまります。

したがって、この位相空間 \( (X, T) \) は非連結です。なぜなら、全体集合と空集合以外にクローペン集合が存在するからです。

この一例だけでも、空間が分離可能であること、つまり連結でないことが明確になります。

次に、実数集合 \( \mathbb{R} \) に標準的な位相を与えます。これは開区間 \( (a, b) \) によって生成される位相です。

この場合、開区間 \( (a, b) \) は開集合ですが閉集合ではなく、閉区間 \( [a, b] \) は閉集合ですが開集合ではありません。

したがって、\( \mathbb{R} \) の中で開かつ閉である部分集合は、全体集合 \( \mathbb{R} \) と空集合 \( \emptyset \) だけです。

このことから、標準位相をもつ実数直線 \( \mathbb{R} \) は連結空間であることがわかります。

次に、部分空間 \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) を考えます。ここでは、標準位相から誘導位相を受け取ります。

この空間では、部分集合 \( (0,1) \) と \( (2,3) \) はどちらも \( X \) において開集合であり、同時に閉集合でもあります。なぜなら、それぞれの補集合がもう一方の開区間になっているからです。

したがって、これらの部分集合はどちらもクローペン集合です。

このように、非自明な開集合かつ閉集合が存在するため、部分空間 \( X \) は非連結です。

言い換えれば、\( X \) は二つの交わらない非空な開集合 \( (0,1) \) と \( (2,3) \) の和として表され、全体が分離されているのです。