任意の連結な部分集合は,ある一つの連結成分に含まれる
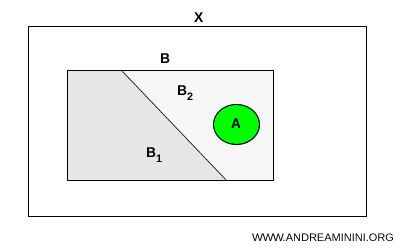
位相空間 \( X \) の部分集合 \( A \) と \( B \) を考える。\( A \) が連結で、かつ \( A \subset B \) が成り立つとする。もし \( B \) が \( X \) において二つの部分集合 \( B_1 \) と \( B_2 \) に分離できるならば、\( A \) はそれらのうちのいずれか一方に完全に含まれなければならない。すなわち、次が成立する。$$ A \subset B_1 \quad \text{または} \quad A \subset B_2 $$
要点は単純である。連結な集合は、分離の両側に同時にまたがることができない。
ある集合が互いに交わらない二つの部分集合に分かれているとき、その内部にある連結な部分集合は、必ずどちらか一方に全体として含まれる。
直感的には、連結集合は切れ目のない一本のロープにたとえられる。このロープを封筒の中に入れ、封筒だけを二つの独立した区画に分けたとしよう。ロープが無傷である限り、それは必ずどちらか一方の区画に収まる。もし両方にまたがるなら、ロープは途中で切れてしまうはずである。連結性とは、このように集合が分離を横断することを許さない性質である。
具体的な例
具体例として、位相空間
$$ X = \mathbb{R} $$
を考え、その部分集合
$$ B = (-3,4) $$
を取る。この集合は次の二つの部分集合に分けることができる。
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
これらは互いに交わらず、
$$ B_1 \cap B_2 = \varnothing $$
その和集合は \( B \) 全体に一致する。
$$ B_1 \cup B_2 = B $$
さらに、\( B_1 \) と \( B_2 \) は \( B \) に誘導される部分空間位相において開集合である。したがって、これらは \( X \) における \( B \) の分離を与えている。
ここで、\( B \) の連結な部分集合として
$$ A = (1,2) $$
を考えると、\( A \subset B_2 \) が成り立ち、\( A \) は分離の一方に完全に含まれていることが分かる。
注。一方、\( A = (-1,1) \) とすると、$$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ となる。しかし、このような状況は起こりえない。なぜなら、\( B_1 \) と \( B_2 \) は \( B \) の分離であり、連結な部分集合がその両方に分かれて含まれることは不可能だからである。仮にそれが可能であれば、\( A \) 自身が分離をもつことになり、区間 \( (-1,1) \) が連結であるという基本事実に反する。重要なのは、\( (-1,1) \) の連結性ではなく、このように分離された \( B \) の中には全体として含まれ得ないという点である。
証明
仮定
位相空間 \( X \) の部分集合 \( A \) と \( B \) に対して、
$$ A \subset X \quad \text{かつ} \quad B \subset X $$
が成り立ち、次を仮定する。
- \( A \) は連結である
- \( A \subset B \) が成り立つ
- \( B_1 \) と \( B_2 \) は \( X \) における \( B \) の分離である
主張
このとき、\( A \) は \( B_1 \) または \( B_2 \) のいずれか一方に含まれる。
$$ A \subset B_1 \quad \text{または} \quad A \subset B_2 $$
証明
\( B_1 \) と \( B_2 \) が \( B \) の分離であることから、次が成り立つ。
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) と \( B_2 \) は \( B \) に誘導される部分空間位相で開集合である
背理法により、\( A \) が \( B_1 \) にも \( B_2 \) にも完全には含まれないと仮定する。
$$ A \cap B_1 \neq \varnothing \qquad \text{かつ} \qquad A \cap B_2 \neq \varnothing $$
\( A \subset B \) であるから、
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
が成り立つ。\( B_1 \) と \( B_2 \) は互いに交わらないため、\( A \cap B_1 \) と \( A \cap B_2 \) も互いに交わらない。
したがって、これら二つの集合は、互いに素で空でなく、かつ \( A \) に誘導される部分空間位相において開集合である。よって、\( A \) は分離をもつことになり、連結であるという仮定に反する。
以上より仮定は誤りであり、結論として
$$ A \subset B_1 \quad \text{または} \quad A \subset B_2 $$
が従う。これで証明は完了である。
以下同様。