共通部分をもつ集合族の連結性

位相空間 \( X \) において，部分集合 \( C_1, C_2, \dots, C_n \subset X \) がすべて連結であり，しかも少なくとも一点を共通にもつとする。すなわち，

\[
\bigcap_{i=1}^n C_i \neq \varnothing . \]

このとき，それらの和集合 \( \bigcup_{i=1}^n C_i \) もまた連結である。

言い換えれば，複数の連結集合が一点でも共有していれば，全体としても連結性は保たれる。

この事実は直感的にも理解しやすい。共通点が存在することで，それぞれの集合が互いに「つながっている」からである。

注。条件 \( \bigcap_{i=1}^n C_i \neq \varnothing \) は，連結性を保証するための十分条件であるが，必ずしも必要ではない。実際には，すべての集合が同一点を共有していなくても，全体として連結となる場合がある。典型的なのが，集合どうしが鎖状に交わる場合である。

具体例

次の \( \mathbb{R}^2 \) の部分集合を考えてみよう。

• \( C_1 \)：点 \( (-1,0) \) から \( (1,0) \) までの水平線分
• \( C_2 \)：点 \( (0,-1) \) から \( (0,1) \) までの垂直線分
• \( C_3 \)：点 \( (-1,-1) \) から \( (1,1) \) を結ぶ対角線分

これらはいずれも連結な集合である。

さらに，いずれも点 \( (0,0) \) を含んでいる。すなわち，

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

したがって，共通部分は空ではない。

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

このことから，連結性の基準により，それらの和集合は連結であることが分かる。

\[ C_1 \cup C_2 \cup C_3 \]

三つの線分はいずれも同一点で交わっており，この構造によって全体が一つにつながっている。

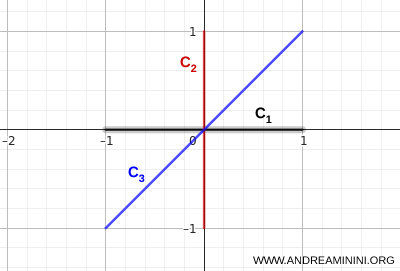
この集合では，どの点から出発しても，集合の内部を通って別の任意の点へ連続的に到達することができる。

注。すべての集合が共通点をもつ必要はない。例えば，各集合が連結であり，かつ \( C_i \cap C_{i+1} \neq \varnothing \) を満たすように鎖状につながっていれば， \( \bigcap_i C_i = \varnothing \) であっても，その和集合は連結となる。さらに，この「鎖状のつながり」も必要条件ではない。場合によっては，いくつかの集合が橋渡しの役割を果たすことで，全体として連結性が保たれることもある。例えば，三本の線分が三角形を形作る場合がその典型例である。このとき，全体の共通部分は空であるにもかかわらず， 和集合は連結である。

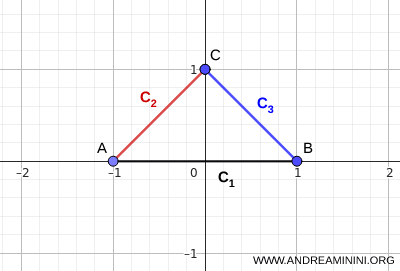
この例は，連結性が必ずしも一点の共有によってのみ保証されるわけではないことを明確に示している。

証明

\( X \) を位相空間とし，\( \{C_i\}_{i \in I} \) をその部分集合族とする。各 \( C_i \) は連結であり，かつ共通部分が空でないと仮定する。

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

ここで，次の集合を考える。

\[ C = \bigcup_{i \in I} C_i \]

これが連結でないと仮定する。

すると，\( C \) は互いに交わらない二つの開集合 \( U \) と \( V \) によって分離される。すなわち，

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

仮定より，共通部分が空でないため，ある点 \( x \) が存在して

\[ x \in \bigcap_{i \in I} C_i \]

を満たす。この点 \( x \) は，分離の定義より，\( U \) または \( V \) のいずれかに属する。一般性を失うことなく，

\[ x \in U \quad \text{かつ} \quad x \notin V \]

と仮定する。

各 \( C_i \subset C \) について，次が成り立つ。

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

ここで，\( C_i \cap U \) と \( C_i \cap V \) は部分空間位相において開集合であり，互いに交わらず，かつその和は \( C_i \) 全体である。しかし，各 \( C_i \) は連結であるため，この二つのうち一方は空でなければならない。

したがって，各 \( C_i \) は \( U \) または \( V \) のいずれか一方に完全に含まれる。

しかし \( x \in C_i \) かつ \( x \in U \) であるため，\( C_i \subset V \) とはなりえない。

よって，すべての \( i \in I \) について

\[ C_i \subset U \]

が成り立つ。

その結果，

\[ \bigcup_{i \in I} C_i \subset U \]

となるが，これは \( V \cap C \neq \varnothing \) という仮定に反する。

以上より仮定は誤りであり，和集合 \( \bigcup_{i \in I} C_i \) は連結であることが分かる。

以上で証明は完了である。