開集合を使って部分集合を分離するとは何か

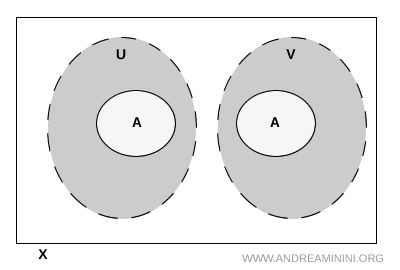
位相空間 $ X $ の部分集合 $ A $ を二つの開集合 $ U $ と $ V $ を使ってきれいに分けることを、ここでは「分離」と呼ぶ。この分離が成立するためには、次の三つの条件がそろっている必要がある。

$ A $ 全体が $ U \cup V $ の中に収まっていること \[ A \subseteq U \cup V \]
どちらの開集合も、必ず $ A $ のある部分とかかわっていること \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
$ A $ の内部では $ U $ と $ V $ が重ならないこと \[ U \cap V \cap A = \varnothing \]

言い換えると、集合 $ A $ は二つのはっきりと分離した部分に分かれ、それぞれが $ U $ と $ V $ の中に入っているという状況になる。これは「その部分集合が位相的に離れている」と説明したいときに使われる、ごく基本的な考え方である。

開集合が部分集合を分離する様子の図

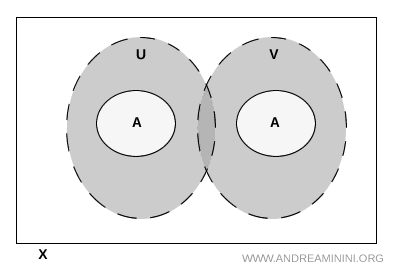
注記. $ U $ と $ V $ が空間全体 $ X $ の中でどこか別の場所で交わっていても問題はない。大切なのは、その交わりが $ A $ の部分に入り込まないという点である。
U と V が A の外側で交わる例の図

具体例で見てみる

直感的に理解しやすいように、実数直線 $ X = \mathbb{R} $ を例にしてみよう。部分集合 $ A $ として、次の二つの離れた閉区間を考える。

$$ A = [-2,-1] \cup [1,2] $$

そして次の二つの開集合を用意する。

$$ U = (-3,0) $$

$$ V = (0,3) $$

これらがどのように配置されているかは、次の図を見ると分かりやすい。

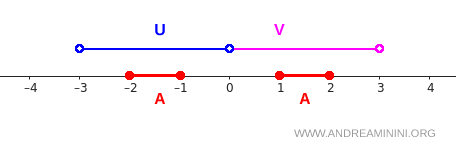
A と開集合 U, V の配置図

まず、区間 $ [-2,-1] $ はすべて $ U $ の中に入っている。逆に、区間 $ [1,2] $ はすべて $ V $ の中に入っている。このため、$ A $ は確かに $ U \cup V $ の内部に収まっている。

それぞれの開集合が $ A $ と実際に交わる点も確認できる。

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

さらに重要なのは、$ U $ と $ V $ が $ A $ の内部では全く重ならないという点である。

$$ U \cap V \cap A = \varnothing $$

これらの条件が全てそろっているので、開集合 $ U $ と $ V $ は実数直線上の部分集合 $ A $ をきれいに分離していると言える。