連結空間とは？

開集合を使った定義

位相空間 $ X $ が 連結（connected） であるとは、空でない2つの開集合 $ U $ と $ V $ が次の3つの条件をすべて満たすような形で存在しないことを意味します。

  • $ U \neq \emptyset $, $ V \neq \emptyset $：どちらも空集合ではない；
  • $ U \cap V = \emptyset $：お互いに交わらない；
  • $ U \cup V = X $：2つを合わせると空間全体になる。

このような組が存在しないとき、空間は連結と呼ばれ、存在する場合は非連結（disconnected）と呼ばれます。

要するに、空間を2つの「バラバラな」開集合に分けて全体を作ることができないなら、その空間は連結だということです。

反対に、もしそんな分け方ができるなら、その空間は非連結であり、その組 $ (U, V) $ は空間 $ X $ の分離（separation）と呼ばれます。

注記. ここで説明しているのは開集合を使った連結性の定義です。この定義は「道連結（path connected）」や「弧状連結（arc connected）」といった他の概念とは異なることがあります。

🔹 具体例で考えてみよう

3つの要素からなる集合 $ X $ を考えます：

$$ X = \{a, b, c\} $$

この集合に、次の2種類の異なる位相を与えます。

  • 位相 A：
    $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
  • 位相 B：
    $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

さて、どちらの空間が連結でしょうか？

定義を思い出すと、連結とは「空でない互いに交わらない開集合で、全体を覆えるような組が存在しないこと」でした。

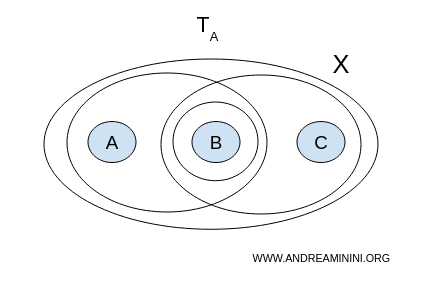
① 位相 A の場合

$ \mathcal{T}_A $ の中で、$ X $ 全体を覆うような空でない開集合の組 $ (U, V) $ を探してみましょう。

  • $ U = \{a,b\}, V = \{b,c\} $ → $ b $ が共通している；
  • $ U = \{a,b\}, V = \{b\} $ → これも交わっている；
  • $ U = \{b\}, V = \{b,c\} $ → 同じく交わっている。

どの組も条件を満たさないため、位相 A における空間 $ X $ は 連結 です。

連結な空間の例

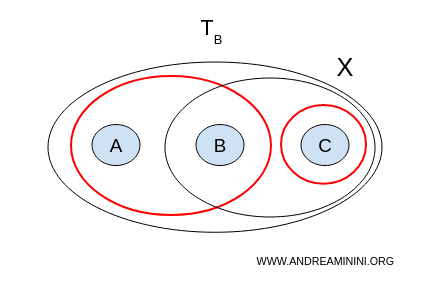
② 位相 B の場合

次に、$ \mathcal{T}_B $ の場合を見てみましょう。

  • $ U = \{a,b\}, V = \{b,c\} $ → $ b $ を共有するので交わっている；
  • $ U = \{a,b\}, V = \{c\} $ → 空でなく、交わらず、和が $ X $ 全体になる。

したがって、この組 $ (U = \{a,b\}, V = \{c\}) $ は完全な分離をつくります。よって、位相 B における空間 $ X $ は 非連結 です。

位相Bにおける非連結空間の例

注記. この例から、連結性は「集合」そのものではなく、「位相の選び方」に依存することが分かります。同じ点集合でも、異なる位相を採用すれば性質が変わります。位相 A では連結、位相 B では非連結です。

🔸 もう一つの例：実数直線から点を1つ除く

実数 $ n $ を固定し、次の集合を考えます（たとえば $ n = 0 $）。

$$ X = (-\infty, n) \cup (n, +\infty) $$

これは「実数直線から点 $ n $ を1つ取り除いた空間」：

$$ X = \mathbb{R} \setminus \{n\} $$

この空間は連結でしょうか？

$ U = (-\infty, n) $, $ V = (n, +\infty) $ を考えます。

  • どちらも通常の実数直線の位相で開集合；
  • 交わらない；
  • どちらも空でない。

その和は $ U \cup V = X $ です。したがって、この空間は定義通り 非連結 です。

注記. 実数直線から1点を取り除くと、その「つながり」が途切れます。点 $ n $ の左側と右側に2つの部分が分かれ、それらを連続的な経路で結ぶことができません。したがって、この空間は非連結であり、同時に道連結でもありません。

🔹 連結空間と道連結空間の違い

「連結」と「道連結」は似ていますが、同じではありません。

  • 連結（topological connectedness）： 空間を2つの空でない開集合に分けて全体を作ることができない。
  • 道連結（path connectedness）： 任意の2点を結ぶ連続的な経路が空間内に存在する。

一般に、道連結な空間は必ず連結ですが、その逆は成り立ちません。

連続的な経路があるということは、その空間が「切り離せない」ことを意味します。しかし、連結であっても経路が存在しない場合があるのです。

例. 有名な例として、トポロジストのサイン曲線（topologist's sine curve） があります。
$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$
この空間は、2つの開集合に分けることができないため連結ですが、振動部分上の点と垂直線上の点を連続的な経路で結ぶことはできません。そのため、道連結ではありません。

このように、連結性と道連結性は似ていても異なる性質であり、位相空間の奥深さを感じさせる概念です。

補足

連結空間に関する補足的な考察

この定理は、位相空間の構造的なつながりを理解するうえで極めて重要な概念を示しています。今後、関連する定理や具体的な例を通じて、連結性という性質がどのように現れるかをさらに詳しく見ていくことができます。

 

 
 
Please feel free to point out any errors or typos, or share suggestions to improve these notes.

FacebookTwitterLinkedinLinkedin

位相空間における連結性