Matematika, Fisika, dan Sains

Topologi

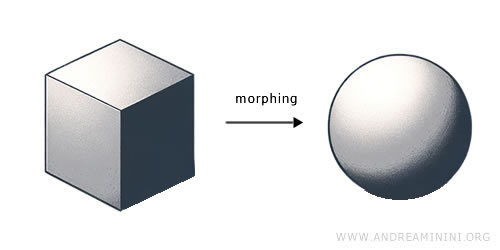
Topologi adalah cabang matematika yang mempelajari sifat-sifat ruang yang tetap terjaga ketika mengalami deformasi kontinu seperti peregangan atau pembengkokan, tetapi tidak sobek atau ditempelkan. Bidang ini membahas konsep seperti kontinuitas, kekompakan, dan keterhubungan, serta sering dijelaskan melalui gagasan himpunan terbuka. Ruang topologi adalah suatu himpunan yang dilengkapi dengan topologi, yaitu kumpulan himpunan terbuka yang memenuhi aksioma tertentu sehingga memungkinkan pendefinisian fungsi kontinu. Topologi berkembang pada awal abad ke-20 dengan kontribusi penting dari matematikawan seperti Henri Poincaré dan Felix Hausdorff. Bidang ini menjadi kerangka dasar bagi banyak cabang matematika dan sains, termasuk analisis, geometri, dan fisika kuantum.

Teori Himpunan

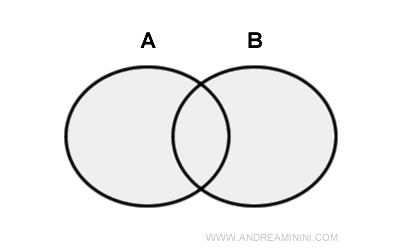
Teori himpunan adalah cabang mendasar matematika yang berfokus pada kajian himpunan, yaitu kumpulan objek yang terdefinisi dengan jelas dan saling berbeda. Objek-objek yang membentuk suatu himpunan disebut elemen atau anggota. Sebuah himpunan dipandang sebagai satu kesatuan yang mencakup semua elemennya. Biasanya, himpunan dilambangkan dengan huruf kapital (A, B, C, ...), sedangkan elemennya ditulis dalam kurung kurawal. Sebagai contoh, himpunan A yang berisi bilangan 1, 2, dan 3 dituliskan sebagai: A={1,2,3}.

Matriks

Matriks adalah susunan bilangan yang teratur dalam baris dan kolom, direpresentasikan sebagai array berbentuk persegi panjang, di mana setiap bilangan disebut elemen matriks. Umumnya, sebuah matriks dilambangkan dengan huruf kapital, misalnya \( A \), dan elemennya ditunjukkan dengan huruf kecil yang memiliki dua indeks, seperti \( a_{ij} \), dengan \( i \) menyatakan baris dan \( j \) kolom. Konsep matriks diperkenalkan pada abad ke-17 oleh matematikawan Inggris James Joseph Sylvester. Namun, pada abad ke-19, Arthur Cayley yang mengembangkan teori matriks modern.

Vektor

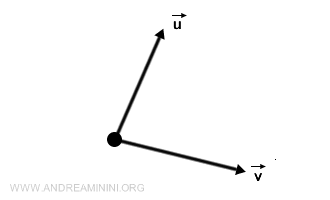Vektor adalah besaran matematika yang memiliki besar (magnitude) sekaligus arah, biasanya digambarkan dengan panah dalam ruang geometri. Dalam notasi, vektor sering ditulis dengan huruf kecil tebal seperti $ \vec{v} $, atau dengan tanda panah di atas huruf, \(\vec{v}\). Vektor dapat dinyatakan melalui komponennya, yaitu proyeksi sepanjang sumbu dalam sistem koordinat. Misalnya, sebuah vektor dua dimensi $ \vec{v} $ dapat dituliskan sebagai \((v_x, v_y)\), dengan \(v_x\) dan \(v_y\) masing-masing komponen pada sumbu x dan y. Konsep vektor sudah dikenal sejak zaman kuno, tetapi matematikawan Prancis Augustin-Louis Cauchy pada abad ke-19 yang merumuskan secara formal dan menggunakannya dalam ilmu fisika serta rekayasa.

Ruang Vektor

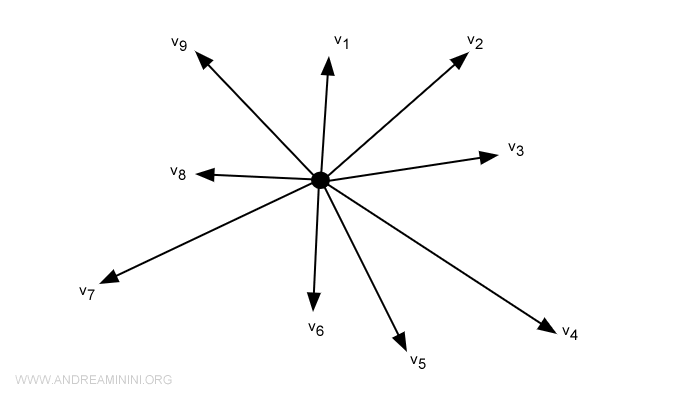Ruang vektor adalah struktur matematika yang dibentuk oleh kumpulan vektor yang dapat dijumlahkan dan dikalikan dengan skalar. Operasi-operasi ini memenuhi aksioma tertentu, seperti asosiativitas, komutativitas, dan distributivitas. Sebuah ruang vektor biasanya dilambangkan dengan huruf kapital, misalnya \(V\), sedangkan elemennya (vektor) dituliskan dengan huruf kecil. Konsep ruang vektor sangat penting dalam aljabar linear karena menyediakan kerangka kerja untuk menganalisis persamaan linear, transformasi, dan pemetaan. Teori modern tentang ruang vektor diformalkan pada abad ke-19 oleh matematikawan seperti Hermann Grassmann dan Giuseppe Peano. Teori ini menjadi dasar bagi matematika dan fisika modern, memberikan struktur yang kuat untuk berbagai aplikasi.

Aljabar Abstrak

Aljabar abstrak adalah cabang matematika yang mempelajari struktur aljabar seperti grup, ring, medan, dan modul. Struktur ini didefinisikan oleh himpunan yang dilengkapi dengan operasi yang mengikuti aksioma tertentu, misalnya tertutup, asosiatif, serta adanya elemen identitas. Aljabar abstrak menyediakan kerangka umum untuk memahami dan menggeneralisasi berbagai sistem aljabar. Bidang ini biasanya dilambangkan dengan huruf kapital seperti \(A\) atau \(B\), sedangkan elemennya dituliskan dengan huruf kecil. Perkembangan aljabar abstrak dimulai pada abad ke-19 dengan karya matematikawan seperti Évariste Galois dan Arthur Cayley, yang memperkenalkan teori grup untuk memecahkan persamaan polinomial. Aljabar abstrak sangat penting dalam banyak cabang matematika dan sains, karena menawarkan alat yang kuat untuk menyelesaikan masalah kompleks dan mengungkap struktur dasar dari berbagai sistem matematis.

Geometri

Geometri adalah cabang matematika yang mempelajari sifat-sifat dan hubungan antar bentuk serta bangun dalam ruang. Bidang ini meneliti titik, garis, bidang, sudut, permukaan, dan bangun ruang, dengan memperhatikan bentuk, ukuran, serta posisi relatifnya. Berdasarkan metode dan alat yang digunakan, geometri terbagi dalam beberapa cabang: geometri Euclidean yang didasarkan pada aksioma Euclid; geometri analitik yang menggunakan sistem koordinat; geometri diferensial yang memanfaatkan kalkulus infinitesimal untuk meneliti kurva dan permukaan; serta geometri non-Euclidean yang perkembangannya mengubah secara mendalam arah matematika dan fisika modern. Asal-usul geometri dapat ditelusuri hingga peradaban Babilonia, Mesir, dan Yunani kuno. Namun, pada abad ke-3 SM, Euclid-lah yang memberikan struktur sistematis pada bidang ini melalui karya besarnya "The Elements". Saat ini, geometri tetap menjadi pilar utama matematika murni sekaligus alat penting dalam banyak disiplin terapan, mulai dari teknik hingga fisika.