Matematik, Fizik ve Bilim

Topoloji

Topoloji, bir uzayın, gerilme ya da bükülme gibi sürekli dönüşümler altında korunan; fakat yırtılma ya da yapıştırma ile bozulabilen özelliklerini inceleyen matematik dalıdır. Süreklilik, kompaktlık ve bağlılık gibi temel kavramlarla ilgilenir ve genellikle açık kümeler aracılığıyla tanımlanır. Bir topolojik uzay, belirli aksiyomları karşılayan açık kümeler ailesiyle donatılmış bir kümedir ve bu yapı sayesinde sürekli fonksiyonlar tanımlanabilir. Topoloji 20. yüzyılın başlarında Henri Poincaré ve Felix Hausdorff gibi matematikçilerin öncülüğünde gelişmiştir. Analizden geometriye, kuantum fiziğinden pek çok uygulamalı alana kadar birçok disiplinde temel bir çerçeve sunar.

Küme Teorisi

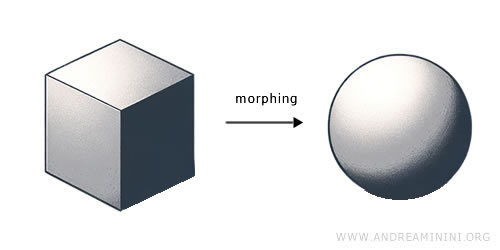
Küme teorisi, matematiğin en temel dallarından biridir ve iyi tanımlanmış, birbirinden ayırt edilebilen nesnelerin oluşturduğu kümeleri inceler. Bu kümelerin içindeki nesnelere eleman denir. Bir küme, tüm elemanlarını tek bir bütün olarak kapsar. Genellikle büyük harflerle (A, B, C, ...) gösterilir; elemanları ise süslü parantezler içinde yazılır. Örneğin 1, 2 ve 3 sayılarından oluşan A kümesi şu şekilde ifade edilir: A={1,2,3}.

Matris

Bir matris, satır ve sütunlar halinde düzenlenmiş sayıların oluşturduğu dikdörtgen biçimli bir tablodur ve her sayı matrise ait bir eleman olarak adlandırılır. Genellikle büyük harflerle (örneğin \( A \)) gösterilir; elemanları ise satır ve sütunu belirten iki indisli küçük harflerle ifade edilir (\( a_{ij} \)). Burada \( i \) satırı, \( j \) sütunu gösterir. Matris kavramı 17. yüzyılda James Joseph Sylvester tarafından ortaya atılmış, ancak modern matris teorisini 19. yüzyılda Arthur Cayley geliştirmiştir.

Vektörler

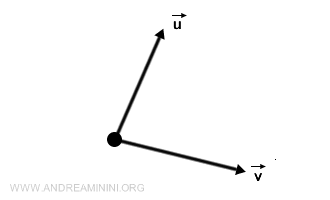Vektör, büyüklüğü ve yönü olan matematiksel bir niceliktir ve genellikle geometrik uzayda bir okla temsil edilir. Gösterimde, çoğu zaman küçük harflerin üzerine ok konularak (\(\vec{v}\)) ya da kalın yazılarak ifade edilir. Vektörler, koordinat eksenleri üzerindeki bileşenleriyle tanımlanır. Örneğin iki boyutlu bir vektör \(\vec{v}\), \((v_x, v_y)\) biçiminde yazılır; burada \(v_x\) x eksenindeki, \(v_y\) ise y eksenindeki bileşendir. Vektör kavramının kökleri eski uygarlıklara dayanır; ancak 19. yüzyılda Fransız matematikçi Augustin-Louis Cauchy, bu kavramı sistematik hale getirerek fizik ve mühendislikteki kullanımını yerleşik hale getirmiştir.

Vektör Uzayı

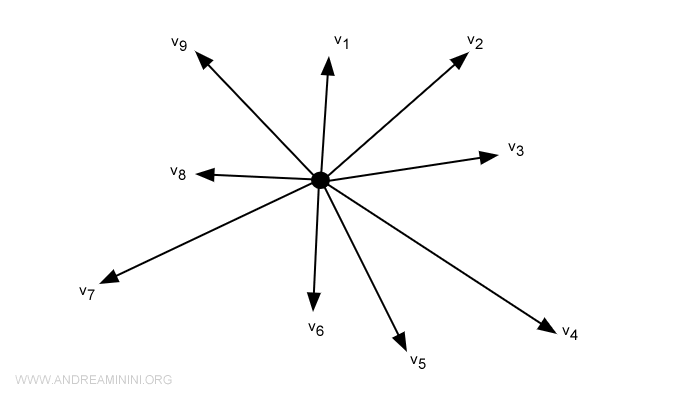Vektör uzayı, vektörlerden oluşan ve bu vektörlerin toplanabildiği, skalerlerle çarpılabildiği matematiksel bir yapıdır. Bu işlemler, toplama ve çarpmanın birleşme, değişme ve dağılım gibi aksiyomlarını sağlar. Genellikle vektör uzayı büyük harflerle (örneğin \(V\)) gösterilir; elemanları yani vektörler küçük harflerle ifade edilir. Vektör uzayı kavramı lineer cebirin temelini oluşturur ve doğrusal denklemlerin, dönüşümlerin ve bağıntıların incelenmesinde çerçeve sunar. Modern vektör uzayı teorisi, 19. yüzyılda Hermann Grassmann ve Giuseppe Peano’nun çalışmalarıyla biçimlenmiş ve günümüz matematiği ile fiziğinde geniş bir uygulama alanı bulmuştur.

Soyut Cebir

Soyut cebir, gruplar, halkalar, cisimler ve modüller gibi cebirsel yapıları inceleyen matematik dalıdır. Bu yapılar, belirli aksiyomları (örneğin kapanış, birleşme, birim elemanın varlığı) sağlayan işlemlerle tanımlanır. Soyut cebir, farklı cebirsel sistemleri anlamak ve genelleştirmek için ortak bir çerçeve sunar. Genellikle bu yapıların gösteriminde büyük harfler (A, B, ...) kullanılır; elemanları ise küçük harflerle ifade edilir. 19. yüzyılda Évariste Galois ve Arthur Cayley, polinom denklemlerini çözmek amacıyla grup teorisini geliştirmiştir. Soyut cebir, matematiğin ve bilimin birçok alanında karmaşık problemleri çözmek ve farklı sistemlerin temel yapısını ortaya çıkarmak için güçlü araçlar sağlar.

Geometri

Geometri, şekillerin ve cisimlerin uzaydaki özelliklerini ve birbirleriyle olan ilişkilerini inceleyen matematik dalıdır. Noktaları, doğruları, düzlemleri, açılar, yüzeyler ve katı cisimleri; biçimleri, boyutları ve konumlarıyla birlikte ele alır. Kullanılan yöntemlere göre farklı alt dallara ayrılır: Öklid’in aksiyomlarına dayanan Öklidyen geometri, koordinat sistemini kullanan analitik geometri, eğri ve yüzeyleri sonsuz küçük hesapla inceleyen diferansiyel geometri ve Öklid dışı geometriler, modern matematik ve fiziğin gelişimini köklü biçimde etkilemiştir. Geometrinin kökleri Babil, Mısır ve Antik Yunan uygarlıklarına kadar uzanır. Ancak MÖ 3. yüzyılda Öklid, ünlü eseri “Elementler” ile bu alana sistematik bir yapı kazandırmıştır. Günümüzde geometri, yalnızca saf matematiğin temel taşlarından biri değil, aynı zamanda mühendislikten fiziğe kadar birçok uygulamalı alanda vazgeçilmez bir araçtır.