数学、物理与科学

拓扑学

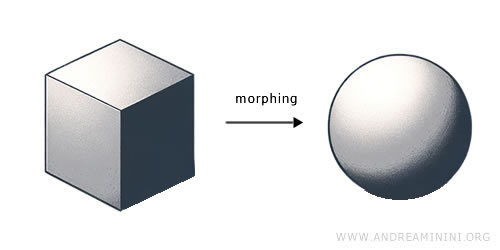
拓扑学是一门研究“形状本质”的数学。它关心的是空间在连续变形（比如拉伸、弯曲）下不变的性质，而不考虑撕裂或粘合。换句话说，拓扑学探讨的是“形状不变”的数学规律。它的核心概念包括连续性、紧致性和连通性，通常用“开集”的思想来表达。一个拓扑空间就是配备了拓扑结构的集合，使我们能够严谨地定义“连续函数”。20世纪初，庞加莱（Henri Poincaré）和豪斯多夫（Felix Hausdorff）等数学家的研究奠定了拓扑学的基础。如今，拓扑思想已经渗透到分析学、几何学甚至量子物理中，是现代科学不可缺少的基石。

集合论

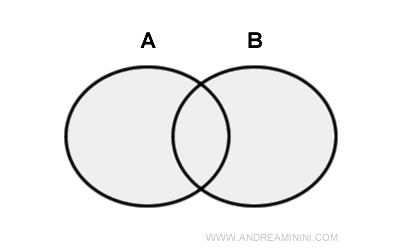
集合论是现代数学的起点。它研究“集合” - - 由清晰且不同的对象组成的整体。集合中的对象叫做元素。我们可以把集合看作一个“容器”，里面放着各种元素。通常用大写字母（A、B、C…）表示集合，元素写在花括号里。例如，包含数字 1、2、3 的集合写作：A={1,2,3}。集合论为整个数学体系提供了统一的语言，就像一张看不见的地图，连接着不同的数学领域。

矩阵

矩阵就像一个整齐排列的数字表格。它由行和列组成，每个数字都叫“矩阵的元素”。矩阵常用大写字母（如 \( A \)）表示，元素记作 \( a_{ij} \)，其中 \( i \) 表示行号，\( j \) 表示列号。17世纪，英国数学家西尔维斯特（James Joseph Sylvester）提出了矩阵的概念；到了19世纪，凯莱（Arthur Cayley）把矩阵理论发展成完整的体系。今天，矩阵已经成为线性代数、计算机科学、物理和工程中的核心工具。

向量

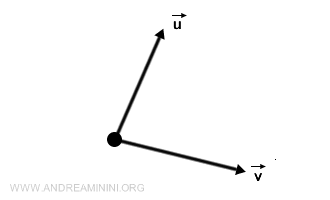向量是一种“既有大小又有方向”的量，可以用一根带箭头的线段来形象表示。我们通常用粗体字母或箭头符号（如 $\vec{v}$ 或 \(\vec{v}\)）表示向量。向量可以通过分量来描述，这些分量反映它在坐标轴上的投影。例如，二维向量 $\vec{v}$ 可以写成 \((v_x, v_y)\)，分别表示在 x 轴和 y 轴上的分量。向量的思想古已有之，但法国数学家柯西（Augustin-Louis Cauchy）在19世纪将它系统化，使其成为物理学和工程学中的基本语言。

向量空间

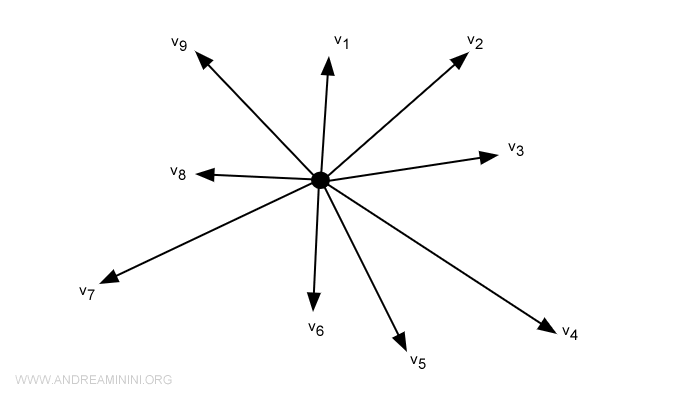向量空间是由一组向量组成的世界。在这里，向量之间可以相加、可以被数相乘，这些运算遵循一系列规则，如结合律、交换律和分配律。通常我们用大写字母（如 \(V\)）表示向量空间，用小写字母表示其中的向量。向量空间是线性代数的核心，帮助我们理解线性方程、变换和映射。19世纪，格拉斯曼（Hermann Grassmann）和皮亚诺（Giuseppe Peano）确立了向量空间理论，它为现代数学与物理提供了统一的思维框架。

抽象代数

抽象代数研究各种代数结构，比如群、环、域和模。它关注的是这些结构内部的运算规律：是否封闭、是否存在单位元、是否满足结合律等。抽象代数让我们能用统一的方式理解不同的代数体系。19世纪，伽罗瓦（Évariste Galois）和凯莱（Arthur Cayley）通过研究多项式方程建立了群论，开创了抽象代数的时代。今天，它不仅是数学的重要分支，也为密码学、物理学和计算机科学提供了强大的理论工具。

几何学

几何学让我们认识空间的形状与结构。它研究点、线、面、角、曲面、立体等对象的性质与相互关系。根据研究方法的不同，几何学分为多个方向：以公理为基础的欧几里得几何；用坐标分析的解析几何；用微积分研究曲线与曲面的微分几何；还有打破传统观念的非欧几里得几何。几何学的起源可以追溯到古巴比伦、古埃及和古希腊，而欧几里得在《几何原本》中让这门学问走向系统化。直到今天，几何学依然是数学的核心语言，也广泛应用于工程、建筑和物理领域。