Математика, физика и наука

Топология

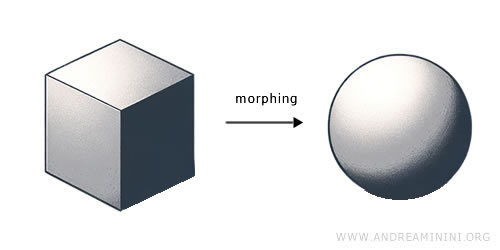Топология - раздел математики, изучающий свойства пространства, которые сохраняются при непрерывных деформациях - растяжении, изгибе, скручивании, но не при разрыве или склеивании. В её основе лежат понятия непрерывности, компактности и связности, формулируемые через систему открытых множеств. Топологическое пространство - это множество, на котором задана топология, то есть совокупность открытых множеств, удовлетворяющих определённым аксиомам и позволяющих строго определить непрерывные функции. Топология сформировалась в начале XX века благодаря работам Анри Пуанкаре и Феликса Хаусдорфа. Сегодня она играет ключевую роль во многих областях математики и физики - от анализа и геометрии до квантовой теории поля.

Теория множеств

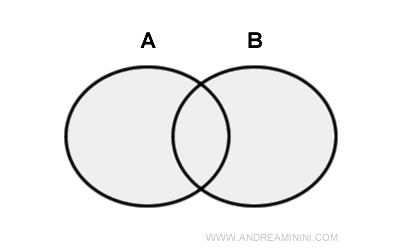
Теория множеств - фундаментальная область математики, изучающая множества как совокупности чётко определённых и различимых объектов. Эти объекты называются элементами множества. Каждое множество рассматривается как единое целое, включающее все свои элементы. Принято обозначать множества прописными буквами (A, B, C, …), а их элементы записывать в фигурных скобках. Например, множество A, состоящее из чисел 1, 2 и 3, записывается так: A={1,2,3}.

Матрица

Матрица - это упорядоченный набор чисел, расположенных в прямоугольной таблице из строк и столбцов. Каждый элемент этой таблицы называется элементом матрицы. Обычно матрицу обозначают прописной буквой, например \( A \), а её элементы - строчной с двумя индексами, \( a_{ij} \), где \( i \) обозначает номер строки, а \( j \) - номер столбца. Понятие матрицы ввёл английский математик Джеймс Джозеф Сильвестр в XVII веке, однако современную теорию матриц разработал Артур Кэли в XIX веке.

Векторы

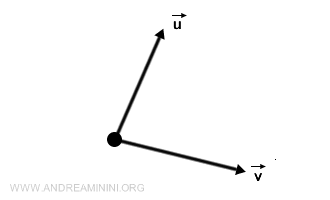Вектор - это математическая величина, обладающая направлением и модулем, обычно изображаемая стрелкой в пространстве. В записи вектор обозначают строчной буквой полужирного начертания, например $ \vec{v} $, или буквой со стрелкой сверху - \(\vec{v}\). Вектор можно задать через его компоненты - проекции на оси координат. Например, двумерный вектор $ \vec{v} $ имеет вид \((v_x, v_y)\), где \(v_x\) и \(v_y\) - проекции на оси x и y соответственно. Хотя идея вектора восходит к античности, строгую математическую форму она получила в XIX веке благодаря трудам французского математика Огюстена-Луи Коши, заложившего основы применения векторов в физике и инженерных науках.

Векторное пространство

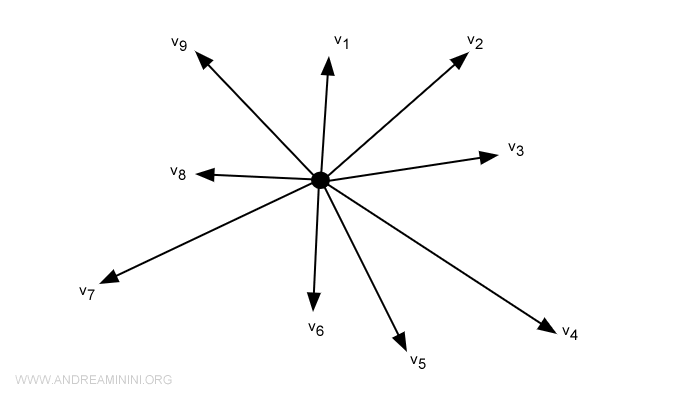Векторное пространство - это математическая структура, состоящая из множества векторов, для которых определены операции сложения и умножения на скаляр, удовлетворяющие определённым аксиомам - ассоциативности, коммутативности и дистрибутивности. Векторное пространство обычно обозначают прописной буквой, например \(V\), а его элементы - строчными. Понятие векторного пространства лежит в основе линейной алгебры и используется при изучении линейных уравнений и преобразований. Современная теория векторных пространств была разработана в XIX веке Германом Грассманом и Джузеппе Пеано. Сегодня она является неотъемлемой частью математики и физики, обеспечивая строгий аппарат для анализа и моделирования различных систем.

Абстрактная алгебра

Абстрактная алгебра - раздел математики, изучающий алгебраические структуры: группы, кольца, поля и модули. Каждая из этих структур определяется множеством, на котором заданы операции, удовлетворяющие определённым аксиомам - замкнутости, ассоциативности, существованию нейтрального элемента и обратного. Абстрактная алгебра создаёт единый язык для описания и обобщения различных алгебраических систем. Обычно такие структуры обозначают прописными буквами \(A\), \(B\), а их элементы - строчными. Современная алгебра возникла в XIX веке благодаря работам Эвариста Галуа и Артура Кэли, которые разработали теорию групп для исследования многочленов. Сегодня абстрактная алгебра занимает центральное место в современной математике и науке, предлагая мощные методы для изучения сложных структур и закономерностей.

Геометрия

Геометрия - это раздел математики, исследующий формы, размеры и взаимное расположение фигур в пространстве. Она изучает точки, прямые, плоскости, углы, поверхности и тела, рассматривая их свойства и взаимосвязи. В зависимости от подхода различают несколько направлений: евклидову геометрию, основанную на аксиомах Евклида; аналитическую геометрию, использующую координатный метод; дифференциальную геометрию, применяющую анализ для изучения кривых и поверхностей; а также неевклидовы геометрии, появление которых радикально изменило современную науку. Истоки геометрии уходят в глубь древности - к вавилонянам, египтянам и грекам, но именно Евклид в III веке до н. э. придал ей строгую логическую структуру в своём знаменитом труде «Начала».