数学・物理学・科学の世界へようこそ

トポロジー（位相幾何学）とは？

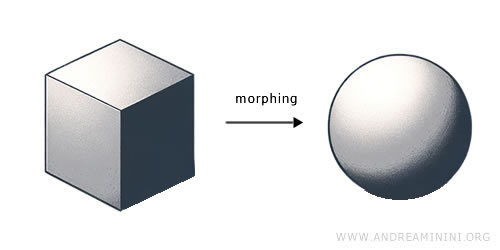
トポロジーは、空間の「形」を根本から考える数学の分野です。たとえば、ドーナツとマグカップは一見まったく違う形ですが、切ったり貼ったりせずに曲げて変形できるという点で“同じ”とみなされます。このように、連続的な変形の下で変わらない性質--連結性、コンパクト性、連続性--を研究するのがトポロジーです。位相空間という概念を使って、開集合の仕組みから空間の構造を論理的に定義します。トポロジーは20世紀初頭、ポアンカレやハウスドルフといった数学者たちによって体系化され、解析学や量子物理学など、さまざまな分野の土台となりました。

集合論 - 数学の基礎

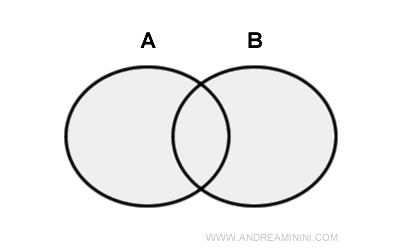集合論は、「ものの集まり」を扱う数学の出発点です。集合を構成する個々の対象は「要素」または「元」と呼ばれます。集合はAやBなどの大文字で表し、その中身を中括弧 { } の中に書きます。たとえば、A = {1, 2, 3} は、1・2・3を要素にもつ集合です。すべての数学の議論は、最終的には集合論の考え方に基づいています。

行列 - 数の並びが生み出す力

行列は、数を行と列に整然と並べた数学的な表です。コンピュータ・グラフィックスから量子力学まで、あらゆる分野で重要な役割を果たしています。行列は通常 \( A \) のような大文字で表され、各成分は \( a_{ij} \) のように添字で示されます。行列の考え方は17世紀にシルヴェスターが導入し、19世紀のアーサー・ケイリーによって現代的な理論へと発展しました。

ベクトル - 向きと大きさをもつ量

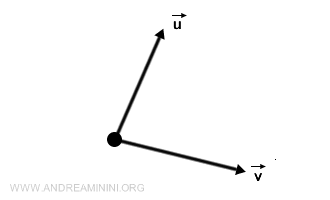ベクトルは「方向」と「大きさ」を同時にもつ量です。たとえば風向きや速度はベクトルで表せます。記号では \( \vec{v} \) のように矢印をつけて書き、2次元なら \((v_x, v_y)\) のように座標軸に沿った成分で表現します。19世紀、フランスの数学者コーシーがこの概念を体系化し、物理学や工学におけるベクトル解析の基礎を築きました。

ベクトル空間 - 数学の共通言語

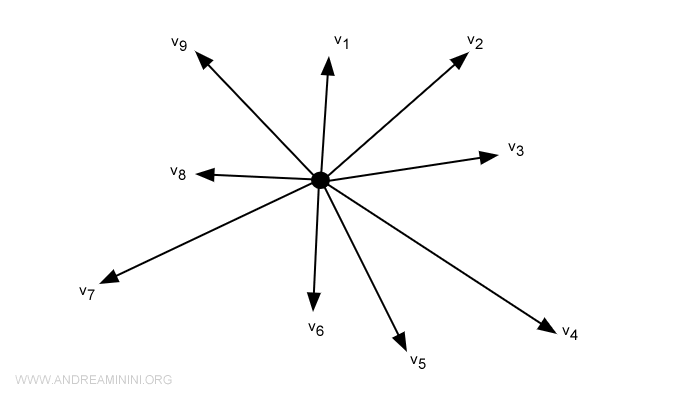ベクトル空間とは、ベクトルの加法とスカラー倍が定義された集合のことです。これらの演算は、結合法則や分配法則といったルールに従います。線形代数学の中心概念であり、線形方程式の解法や写像の解析など、数多くの応用があります。19世紀にグラスマンとペアノが理論を定式化し、現代数学や物理学に欠かせない枠組みを作り上げました。

抽象代数学 - 構造を読み解く

抽象代数学は、群・環・体など、特定の法則に従う「構造」を研究する数学の分野です。加法や乗法といった演算がどのような性質をもつかを一般化し、異なる数学体系を一つの枠組みで理解しようとします。19世紀、ガロアとケイリーが多項式方程式の研究から群論を生み出したことが、その出発点でした。今日では、暗号理論や物理法則の対称性など、幅広い領域で応用されています。

幾何学 - 形の科学

幾何学は、空間に存在する形や構造を研究する学問です。点、線、面、立体などを対象に、それらの関係や性質を探ります。古代ギリシャのユークリッドが著した『原論』によって体系化されたユークリッド幾何学をはじめ、座標を使う解析幾何学、微積分を用いる微分幾何学、さらには非ユークリッド幾何学など、多様な分野に広がっています。幾何学は古代から現代に至るまで、純粋数学の礎であると同時に、工学や物理学など応用科学の中心的ツールでもあります。