수학, 물리학 그리고 과학의 세계

위상수학

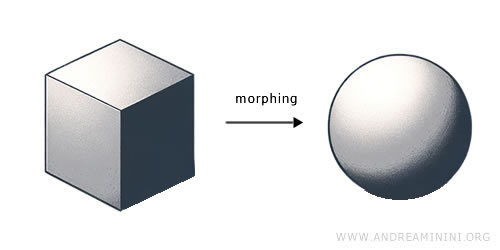
위상수학은 공간을 자르거나 붙이지 않고 늘이거나 구부리는 변형을 통해서도 변하지 않는 성질을 연구하는 흥미로운 수학 분야입니다. 즉, 형태가 조금 달라져도 본질적인 구조가 같다면 그것은 같은 위상적 성질을 가진다고 볼 수 있습니다. 이 분야에서는 연속성, 연결성, 콤팩트성과 같은 개념이 핵심이 되며, 이러한 성질을 설명하기 위해 ‘개방집합’이라는 개념이 사용됩니다. 위상공간은 일정한 규칙(공리)을 만족하는 개방집합의 집합으로 정의되며, 이를 통해 연속함수의 개념을 명확히 다룰 수 있습니다. 20세기 초 앙리 푸앵카레(Henri Poincaré)와 펠릭스 하우스도르프(Felix Hausdorff) 등이 이론을 정립했으며, 오늘날 위상수학은 해석학, 기하학, 양자물리학 등 현대 과학의 기초를 이루는 핵심 이론으로 자리 잡고 있습니다.

집합론

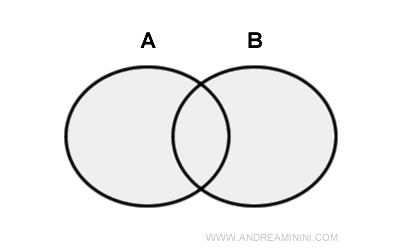집합론은 수학의 언어라고 할 수 있습니다. 명확하게 정의된 대상들의 모임인 ‘집합’을 연구하며, 수학의 거의 모든 분야가 이 개념 위에 세워져 있습니다. 집합을 구성하는 개체를 ‘원소’라고 부르고, 보통 대문자(A, B, C…)로 집합을, 중괄호 안의 항목으로 원소를 나타냅니다. 예를 들어 숫자 1, 2, 3으로 이루어진 집합 A는 A = {1, 2, 3}으로 쓸 수 있습니다. 이 단순한 개념이 함수, 확률, 해석학 등 수많은 수학 이론의 기반이 됩니다.

행렬

행렬은 숫자들을 행과 열로 배열한 구조로, 데이터를 정리하고 연산을 수행하기에 매우 효율적인 도구입니다. 행렬은 대문자 \( A \)로 표시되며, 각 원소는 두 개의 첨자를 사용해 \( a_{ij} \)처럼 나타냅니다. 이 개념은 17세기 제임스 조지프 실베스터(James Joseph Sylvester)가 제안했으며, 19세기 아서 케일리(Arthur Cayley)가 이론을 발전시켜 오늘날 선형대수학의 핵심으로 자리 잡았습니다. 행렬은 컴퓨터 그래픽, 데이터 과학, 양자역학 등 현대 기술과 학문의 거의 모든 영역에서 사용됩니다.

벡터

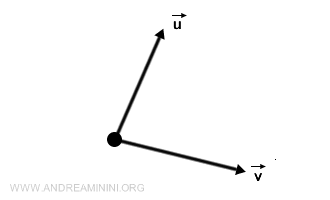벡터는 ‘크기’와 ‘방향’을 동시에 가지는 양으로, 기하학적 공간에서 화살표로 표현됩니다. 보통 굵은 소문자나 화살표 표기, 예를 들어 $\vec{v}$처럼 씁니다. 2차원 벡터는 \((v_x, v_y)\)로 나타내며, \(v_x\)와 \(v_y\)는 각각 x축과 y축의 성분을 의미합니다. 이 단순한 개념이 바로 물리학, 공학, 그래픽스 등에서 힘, 속도, 위치를 설명하는 핵심 언어가 됩니다. 19세기 프랑스의 수학자 오귀스탱 루이 코시(Augustin-Louis Cauchy)가 이를 이론적으로 체계화했습니다.

벡터공간

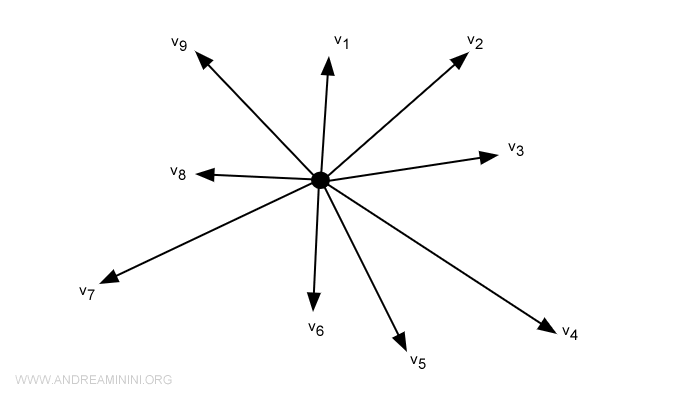벡터공간은 벡터들을 더하거나 스칼라배할 수 있는 수학적 구조입니다. 이러한 연산은 결합법칙, 교환법칙, 분배법칙 등 일정한 규칙을 따라야 합니다. 벡터공간은 대문자 \(V\)로 표시되며, 그 안의 벡터는 소문자로 나타냅니다. 이 개념은 선형대수학의 뼈대이자, 선형방정식이나 선형변환을 이해하는 기본 도구입니다. 19세기 헤르만 그라스만(Hermann Grassmann)과 주세페 페아노(Giuseppe Peano)가 현대적 개념을 확립했으며, 오늘날 물리학, 컴퓨터 비전, 기계학습 등 다양한 분야의 핵심 이론으로 사용됩니다.

추상대수학

추상대수학은 군, 환, 체, 모듈처럼 일정한 규칙을 가진 구조를 연구하는 학문입니다. 이러한 구조는 닫힘성, 결합법칙, 항등원의 존재 등 일정한 공리를 따르며, 복잡한 수학적 시스템을 통합적으로 이해하고 일반화할 수 있는 틀을 제공합니다. 이 분야는 19세기 에바리스트 갈루아(Évariste Galois)와 아서 케일리(Arthur Cayley)의 연구를 통해 발전하였으며, 다항식 방정식의 해법에서 출발해 오늘날 암호학, 양자정보학, 인공지능의 수학적 기반이 되었습니다.

기하학

기하학은 공간 속 점, 선, 평면, 각, 면, 입체 등의 관계와 성질을 탐구하는 수학의 가장 오래된 분야 중 하나입니다. 유클리드의 공리에 기반한 ‘유클리드 기하학’에서부터, 좌표계를 이용한 ‘해석기하학’, 미적분학을 응용한 ‘미분기하학’, 그리고 우주 구조를 이해하는 데 필수적인 ‘비유클리드 기하학’까지 다양한 분야로 발전했습니다. 기하학의 뿌리는 고대 바빌로니아와 이집트, 그리고 그리스의 학문 전통으로 거슬러 올라가며, 기원전 3세기 유클리드(Euclid)가 저술한 『원론(The Elements)』은 지금까지도 수학의 교과서로 여겨집니다. 오늘날 기하학은 순수수학의 중심일 뿐 아니라, 공학, 컴퓨터 그래픽, 물리학, 우주과학 등 수많은 분야에서 활약하고 있습니다.