الرياضيات والفيزياء والعلوم

الطوبولوجيا

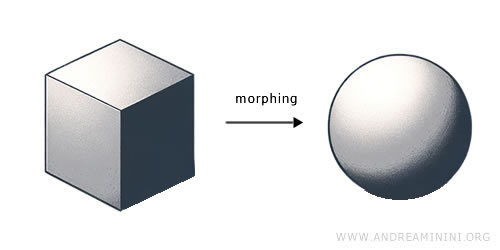الطوبولوجيا، أو ما يُعرف أحيانًا بـ«هندسة المطاط»، هي فرع من فروع الرياضيات يدرس الخصائص التي تبقى ثابتة عند تشويه الأجسام بطرق مستمرة مثل التمدد أو الانثناء، طالما لم يحدث تمزق أو التصاق. تُعنى الطوبولوجيا بمفاهيم مثل الاتصال والاستمرارية والانضغاطية، وتُعرَّف من خلال المجموعات المفتوحة. يُسمّى الفضاء الطوبولوجي أي مجموعة مزوّدة بطوبولوجيا محددة تُمكّن من دراسة الدوال المستمرة والعلاقات البنيوية بين النقاط. نشأ هذا العلم في أوائل القرن العشرين على يد علماء مثل أنري بوانكاريه وفليكس هاوسدورف، وأصبح اليوم أداة أساسية في فهم العديد من الظواهر الرياضية والفيزيائية، من التحليل إلى ميكانيكا الكم.

نظرية المجموعات

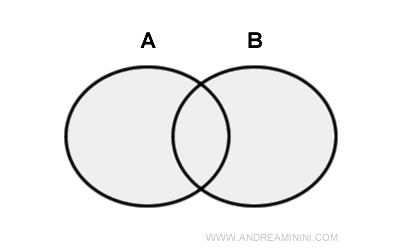تُشكّل نظرية المجموعات حجر الأساس لكل فروع الرياضيات الحديثة. فهي تدرس طبيعة «المجموعة» بوصفها تجميعًا من العناصر المحددة والواضحة. تُكتب المجموعات عادة بأحرف كبيرة مثل (A، B، C...)، وتُعرض عناصرها بين أقواس معقوفة، مثل: A={1,2,3}. رغم بساطتها الظاهرية، إلا أن نظرية المجموعات هي الإطار الذي يُبنى عليه معظم البناء الرياضي، من الأعداد إلى التحليل والدوال.

المصفوفات

المصفوفة هي جدول من الأعداد مرتبة في صفوف وأعمدة، تُستخدم لتمثيل البيانات والعلاقات الرياضية بطريقة منظمة. يُشار إليها عادة بحرف كبير مثل \(A\)، بينما تُكتب عناصرها الصغيرة مع مؤشرات مثل \(a_{ij}\)، حيث \(i\) رقم الصف و\(j\) رقم العمود. ظهرت فكرة المصفوفات في القرن السابع عشر، لكن آرثر كايلي في القرن التاسع عشر وضع أسسها الحديثة. اليوم تُعد المصفوفات أداة لا غنى عنها في الجبر الخطي، والفيزياء، وعلوم الحاسوب، ومعالجة الصور، والذكاء الاصطناعي.

المتجهات

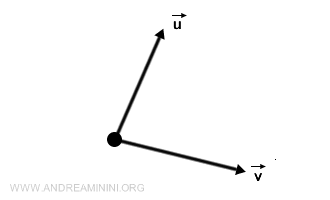المتجه هو كمية تمتلك مقدارًا واتجاهًا، ويُعبَّر عنها بسهم في الفضاء. نستخدم المتجهات لتمثيل السرعة والقوة والإزاحة وغيرها من الكميات الفيزيائية. يُرمز لها غالبًا بـ \( \vec{v} \)، ويمكن تمثيلها بمركبتين في بعدين مثل \((v_x, v_y)\)، أو بثلاث مركبات في الفضاء ثلاثي الأبعاد. لعب العالم الفرنسي أوغستين-لويس كوشي دورًا محوريًا في تطوير هذا المفهوم في القرن التاسع عشر، الذي أصبح أساسًا في الفيزياء والهندسة والتحليل الرياضي الحديث.

الفضاءات المتجهية

الفضاء المتجهي هو عالم واسع تُجرى فيه عمليات الجمع والضرب بين المتجهات والأعداد، ضمن قواعد دقيقة تسمى «بديهيات». يُمثل عادة بحرف كبير مثل \(V\)، وتُعبّر عناصره عن متجهات يمكن استخدامها لنمذجة الظواهر الخطية وتحليل البيانات. من خلال الفضاءات المتجهية يمكننا فهم المعادلات الخطية والتحويلات، وهي الأساس الذي يقوم عليه الجبر الخطي. وضع هيرمان غراسمن وجوزيبي بيانو اللبنات الأولى لهذا المفهوم في القرن التاسع عشر، ولا تزال الفضاءات المتجهية حتى اليوم لغة الرياضيات الحديثة والفيزياء النظرية.

الجبر المجرد

يذهب الجبر المجرد إلى ما هو أبعد من المعادلات، ليدرس البنى التي تحكمها مثل الزمر والحلقات والحقول. تُعرَّف هذه البنى بمجموعة من العمليات والقواعد التي تتيح دراسة العلاقات الرياضية بطريقة موحّدة. بدأ هذا الفرع مع أعمال إيفاريست غالوا وآرثر كايلي في القرن التاسع عشر، عندما استخدما نظرية الزمر لحل المعادلات متعددة الحدود. ومنذ ذلك الحين أصبح الجبر المجرد أحد أعمدة الرياضيات النظرية، إذ يقدّم أدوات قوية لفهم الأنظمة الرياضية وتطبيقاتها في الفيزياء، وعلم الحاسوب، ونظرية الشفرات.

الهندسة

الهندسة هي العلم الذي يدرس الأشكال والعلاقات المكانية بينها - من النقاط والخطوط إلى الأجسام الصلبة في الفضاء. فهي تجمع بين الجمال والمنطق، وتُعد من أقدم فروع الرياضيات. تشمل الهندسة الإقليدية القائمة على مسلّمات إقليدس، والهندسة التحليلية التي تستخدم الإحداثيات، والهندسة التفاضلية التي تعتمد على التفاضل والتكامل لدراسة المنحنيات والأسطح، والهندسات اللاإقليدية التي غيرت نظرتنا إلى المكان والزمن. بدأت جذور الهندسة في الحضارات القديمة، لكن إقليدس في القرن الثالث قبل الميلاد وضع لها الأساس العلمي في كتابه الشهير «العناصر». واليوم تظل الهندسة لغة أساسية في الرياضيات والعلوم والتكنولوجيا، من تصميم الجسور إلى فهم الكون نفسه.